정렬 (Sorting Algorithms)

다음의 문제를 가지고 선택, 삽입 정렬에 대해 알아보고 장단점을 파악해보자

문제: 리스트 안에 있는 자료를 오름차순으로 정리 입력 예 : [35,2,9,85,17] 출력 예 : [2,9,17,35,85]

선택정렬 (Selection sort)

선택 정렬은 매순간 최소값을 선택해 정렬한다. 예시를 통해 알아보면

  1. [35,2,9,85,17] 에서 n개를 비교해 최소값(2)을 찾는다. -> 최소값과 첫번째 위치의 순서를 바꾼다.

         1의 결과: [2,35,9,85,17]

  2. [2,35,9,85,17] 에서 첫째항 제외한 n-1개 에서 최소값(9)을 찾는다. -> n-1개의 값과 9를 비교하여 결정

        2의 결과: [2,9,35,85,17]

  3. 위의 과정을 총 n번 반복하여 정렬을 완료한다.

선택 정렬의 특징

운동장에서 무작위로 서있는 학생들을 키 순서로 세울 때 키가 가장 작은 애를 찾고 그다음 작은 애를 찾고 하는 방식을 반복하는 것과 같다.

  • 장점 일반적으로 생각하기 쉽고 구현이 쉽다. 총 정렬회수를 미리 예측 가능하다.
  • 단점 시간복잡도를 생각했을 때 T(n) = (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2) 이므로 입력이 커질수록 정렬하는 데 오랜 시간이 걸린다.

삽입정렬 (Insertion sort)

삽입정렬은 선택정렬과 달리 선택할때 비교를 하고 선택하는 것이 아니라 선택을 먼저 하고 비교를 한다. 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬한다. 예시를 통해 알아보면

  1. [35,2,9,85,17]에서 두번째 자료인 2 부터시작한다. 2와 35를 비교해 2가 더 작으므로 바꾼다.

    1의 결과 : [2, 35, 9, 85, 17]

  2. [2, 35, 9, 85, 17] 에서 세번째 자료인 9를 선택하고 9와 그 전항인 35를 비교해 9가 더 작으므로 자리를 옮긴다. 그 이후 9와 그 전항인 2를 비교해 2가 더 작으므로 둘의 자리를 바꾸지 않는다.

    2의 결과 : [2,9,35,85,17]

  3. [2,9,35,85,17] 에서 네번째 자료인 85를 선택하고 전항인 35와 비교해 35가 더 작으므로 자리를 옮기지 않고 끝낸다.

    3의 결과 : [2,9,35,85,17]

  4. [2,9,35,85,17] 에서 다섯번째 자료인 17을 선택하고 전항인 85와 비교해 더 작으므로 자리를 옮긴다. 이후 그 전항인 35와 비교해 더 작으므로 자리를 옮긴다. 다시 그 전항인 9와 비교해 더 크므로 자리를 유지하고 끝낸다.

    4의 결과 : [2,9, 17, 35, 85] 종료.

삽입 정렬의 특징

최상의 경우일때, 예를 들어 [1,2,3,4,5]를 정렬한다고 하면 n-1개의 항을 한번 씩만 비교하면 되기에 시간복잡도는 O(n)이다. 하지만 최악의 경우 때 시간복잡도는 선택정렬과 같이 O(n**2) 이다.

  1. 장점
    • 대부분이 이미 정렬되어 있는 경우 효율적일 수 있다.
    • 구현하고 생각하기 쉽다.
  2. 단점
    • 대부분의 경우에서 시간이 오래걸린다.(비효율적)
    • 많은 값들의 이동이 있다.

병합정렬 (Merge sort)

분할 정복의 일종으로 다음과 같은 분할 정복의 특징을 가진다.

  1. 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결한다.
  2. 이 과정에서 일반적으로 재귀(recursion)을 이용한다.

    과정

  3. 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
  4. 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
  5. 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

병합 정렬의 예

[6,8,3,9,10,1,2,4,7,5]을 병합정렬을 이용해 오름차순으로 정리해보자.

  1. 두개의 그룹(g1,g2)으로 나눈다. (분할)

    g1 = [6,8,3,9,10] g2 = [1,2,4,7,5]

  2. g1 과 g2를 각각 오름차순으로 정렬 (1~6 재귀를 이용)

    g1 = [3,6,8,9,10] g2 = [1,2,4,5,7]

  3. 이제 두 그룹을 하나의 그룹으로 만든다. (병합) 두 그룹의 첫 번째 값을 비교하여 작은 값을 빼 결과 리스트에 추가한다.

     g1 = [3,6,8,9,10] g2 = [2,4,5,7] result = [1]

  4. 다시 두 그룹의 첫 번째 값을 추가해 결과리스트에 추가한다.

     g1 = [3,6,8,9,10] g2 = [4,5,7] result = [1,2]

  5. 위를 반복하여 한 그룹이 빈 배열이 될 때 까지 반복한다.

     g1 : [8,9,10] g2 = [] result = [1,2,3,4,5,6,7]

  6. 빈 배열이 아닌 배열 의 남은값들을 result에 추가하여 끝낸다.

    g1 : [] g2 = [] result = [1,2,3,4,5,6,7,8,9,10]

종료

병렬 정렬의 특징

  • 장점 – 시간복잡도가 O(n * log n)으로 상대적으로 많은 시간을 줄일 수 있다. 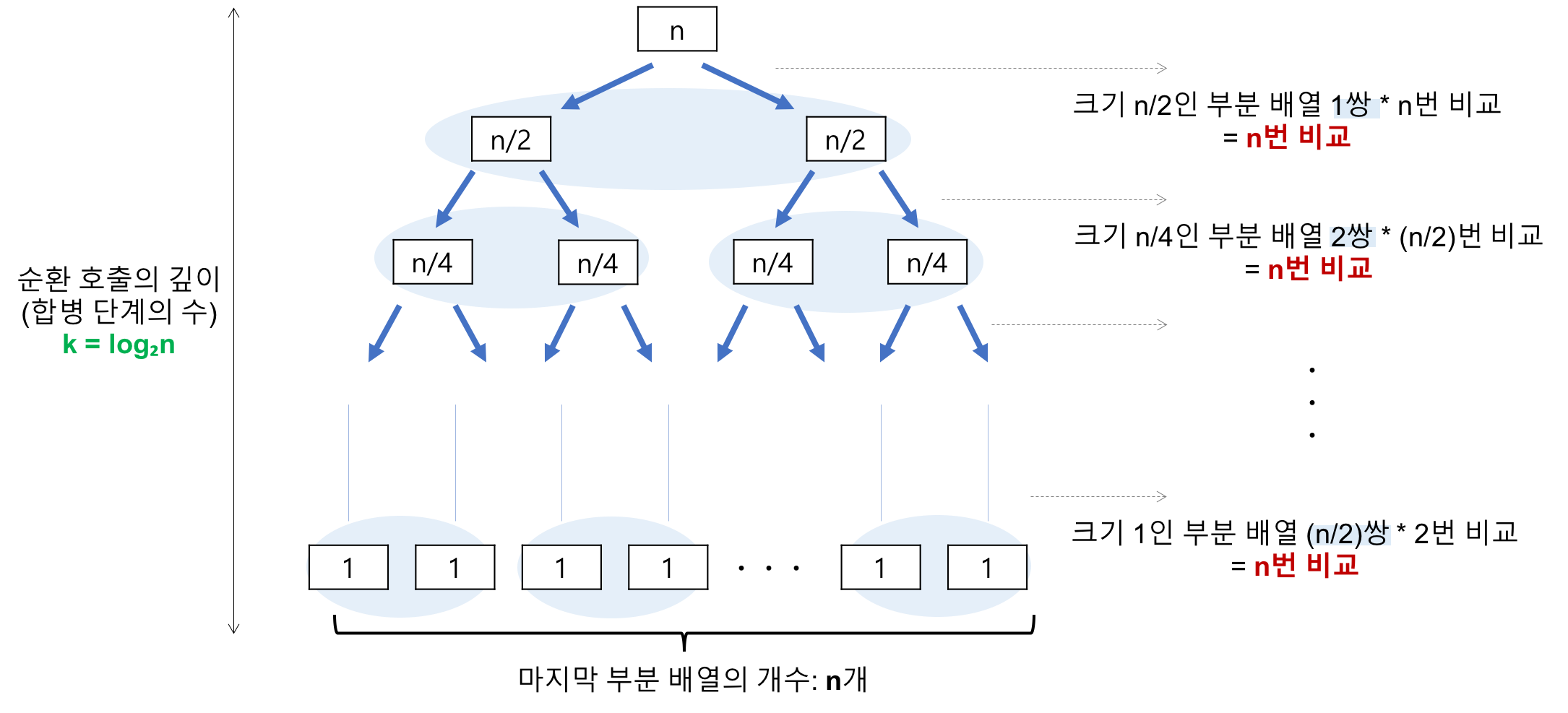출처 :[알고리즘] 합병 정렬(merge sort)이란
  • 단점 – 고려해야할 요소가 상대적으로 많다.(재귀의 종료조건, 분할)